Apologies for a newbie question: I am very new to the topic of GA.
I’m carefully following along with “Imaginary Numbers are not Real” (Gull, Lasenby and Doran). It all makes sense but I’ve hit a bump in the road with section 3 (Rotations), equation (10):
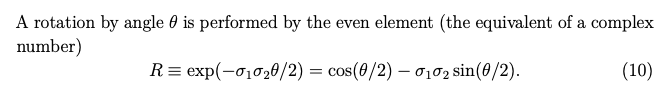
I’m familiar with Euler’s formula in the normal sense; and I (more or less) follow the paper’s earlier point that the highest grade element (‘pseudoscalar’) commutes with everything and squares to minus 1. I have also noted that a Rotor contains even-grade elements and is therefore ‘like a complex number’. But it feels like a bit of a leap of faith to exponentiate a multivector.
I readily admit that my question perhaps shows that I should reexamine the derivation of Euler’s identity… but some assistance with this step would be greatly appreciated!
Thanks in advance
Martin
Hi! To find out what I can do, say @discobot display help.
OK I think my confusion arose from trying to apply a geometric interpretation to the idea of exponentiation of a pseudoscalar.
I should instead consider exponentiation as the algebraic operation:
e^z=\frac{z^0}{0!}+\frac{z^1}{1!}+\frac{z^2}{2!}+\dots
Things now make more sense: GA tells us how to multiply multivectors and therefore to form z^n.
Euler’s formula now follows from the expansions of the exponential and trigonometric functions, with the powers of the pseudoscalar alternating in sign as usual.
Exactly! To see how the terms add visually, you might want to check this little example I wrote: exp (the x position of the mouse is the argument, and you can choose the square of the element of the algebra to be +/-1 to get a hyperbolic/circular geometry).
Oooooh - that’s great! What do the colours signify?
For the record, I got a bit stuck extending the 2D case to higher dimensions. However with a little help I arrived at:
\begin{align}
e^{ia}=\sum_{k=0}^\infty\frac{i^ka^k}{k!}&=\sum_{k\text{ even}}+\sum_{k\text{ odd}}\\
&=\sum_{r=0}^\infty\frac{i^{2r}a^{2r}}{(2r)!}+\sum_{r=0}^\infty\frac{i^{2r+1}a^{2r+1}}{(2r+1)!}\\
&=\sum_{r=0}^\infty\frac{(-1)^ra^{2r}}{(2r)!}+i\Big(\sum_{r=0}^\infty\frac{(-1)^{r}a^{2r+1}}{(2r+1)!}\Big)
\end{align}
Evidently (3) has the form \cos()+i\sin() but the arguments look problematic.
Fortunately a^{2r}=(aa)^r=\lvert a\rvert^{2r} comes to our rescue, giving:
e^{ia}=\cos(\lvert a\rvert)+i\tfrac{a}{\lvert a\rvert}\sin(\lvert a\rvert)
Thanks! I wrote it for myself and yours is the first feedback I get 
The colors of the lines are arbitrary, just to show the different parts/pieces of the sum.
By the way, you can zoom in/out with the mouse wheel too.
In case you are curious, the code comes from Jordi / exp · GitLab . It is a simple test to play with Geometric Algebra visuals, and to learn ClojureScript and how to use both quil to draw and reagent-material-ui to build a modern interface. A more powerful related project is Jordi / Geometric Algebra · GitLab .
Yes, all this looks right. Note that you don’t need to use i a, you can just use a (which can be any multivector whose square commutes with itself – in particular any 1-vector). At the end you can substitute a = i x to find the original Euler formula.
Well… with sin and cos if a^2 < 0, and sinh and cosh if a^2 > 0.
(And 1 + x if a^2 == 0  )
)