Wow. This is where I was really sort of heading next I suppose…
I thought my axis-angle scaled was making headway 
(Really angle-angle-angle) which really is a vector space that projects to quaternions/matrices/etc; but loses anything translational.
I made this wolfram cloud notebook of just some math…
There are a few things I’ve come across that are lost in the simplicity of your math though.
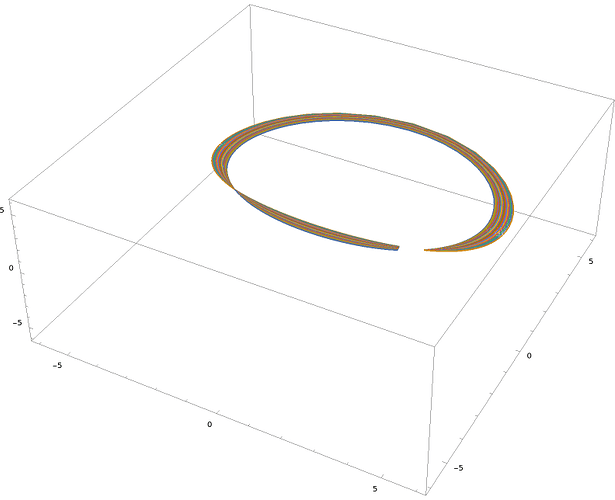
For example, this is a geodesic curve over 4pi rotations, such that the normal pole is actually 180 degrees from the origin; then the magnitude of 360 degrees between that orientation and the same orientation and the other 360 degrees have a different magnitude.
(showing the scaled axis*angle coordinates)
Rotors I see are somewhat similar, but I don’t actually consider them a bi-vector… they’re a rotation around an axle. (A axis on a wheel would be more properly named axle, no? as an axis of rotation ) , and rotation vectors are 3 angles around the X Y and Z axes (axles) that’s how much around each of those a rotation happens; and the composite 3D vector is just the angles, but the resulting vector has a direction that’s also the axis of rotation for the composition of those 3 into a single rotation. ( You’re quite confident in the 6D rotational coordinate for 4D, so that’s great, I think I’d love to invest in your math Because there are 6 basic rotation coordinates you would need, I’m just not sure how the X->W, Y->W and Z->W rotations all end up moving W in a sensible way, but I’d imagine I can play with your stuff and get useful information )
Rotation vectors, unlike quaternions, don’t need any special projective geometry consideration, you don’t have to shine the line from the rotation vector through the quaternion into a hypersphere… and even though a quaternion has 4 coordinates, it’s (for rotations) only a 3D thing; where rotation itself rarely requires an elevation (or radial offset from the curves).
I have this project… that is based around the Rodrigues Rotation Formula… I did do some considerations of averaging rotations, you end up having to translate a family that you want to average to the origin , average, and then rotate back into the right place… works pretty well (would share link, but limited - index-normals.html) other than places where the mesh generation has no good information for the normal direction… a surface that’s a pyramid half offset makes the surfaces exactly line up with points in space, and there’s not enough precision between 0 to 0 to get a good direction. (github d3x0r dualmarchingtetrahedra) which is this other side project just for getting a mesh from a point cloud using a mesh of tetrahedra on a cubic lattice)
But - I end up with a smooth function for rotations that allows multiplying by a time factor… and I’m sort of stuck in 3D because there’s no evidence we might have a 4th spatial dimension
But - I do also expect you’re standard rotations are extrinsic? This will annoy me to no end, because usually moving forward you’re more interested in intrinsic rotations ; like propagating down a chain… I end up with a single cross product I can reverse to change between intrinsic and extrinsic without reversing operands… but then that also led me to have 3D for rotations and 3D for linear motion, making a nice 7D universe including time…
But then; I was playing with curvature, and parallel transporting vectors and all that; and had an insight ‘what if space is really curved by mass’ and that the sum of all the displacements from each nucleus of each atom contributes to the overall displacement… which in large scale effect you’d notice a smooth field that’s the average of the gravity; and then you can apply space displacements without time, and have a static gravitational field for light geodesics… Light geodesics and Matter Geodesics are different… Light doesn’t curve, so any curvature that it experiences must be positive, otherwise behind a black hole an arc of the sky behind it would be hidden; and even around our own sun- the Eddington experiment would have failed…
(and for my second link, I guess this is the best starting point, it gets to the interactive demos with sliders and stuff)
Stretching Space
And then, what if space is curved as in a change in distance over distance, and it doesn’t require any change in time (which it doesn’t, over very long distances, the mass displacement of all the galaxies that light doesn’t go through results in a overall stretching of the space…
There is a minor question in the previous thing though… space would have to be stretched by the furthest sources first, before the nearest, so space can otherwise flow around the points of displacement… but then the universe is in a flat space, where only light-space (or Maxwell’s Aether? ) is bent… But also, there’s the spatial gradient that causes red shift and blue shift in non-accelerating bodies like Pound-Rebka. And recently space dot com posted an article about measuring the curature of space with a particle fountain.
But great job; off to learn more…