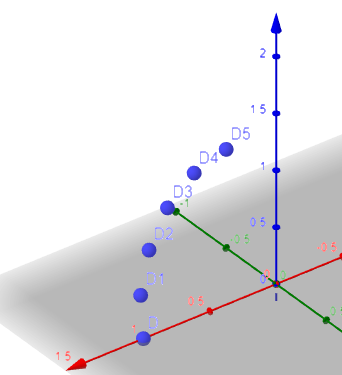
I wanted to understand interpolation between two rotors so I made a simple example where a point D is supposed to be rotated. The positions D1-D5 have negative y coordinates which can be seen on the image. I expected that, since R1 rotates CW by 30 deg and the other CCW by 90 deg, the successive positions of D would all have +ve coordinates.
Also, below I am not sure if this is a correct way to find nth root of R. Once half angle is obtained, I divided LogR_n with it to obtain “I” for computing the exponential.
Rotor(Zax,30) → R1= 0.9659258 + -0.258819e12
Rotor(Yax,-90) → R2= 0.7071068 + 0.7071068e31
D= (1.0, 0.0, 0.0)
R1 * D * ~R1= (0.8660254037844387, 0.49999999999999994, 0.0)
R2 * D * ~R2= (0.0, 0.0, 1.0000000000000002)
rrrrr*R1= 0.7071068 + 0.7071068e31
R2= 0.7071068 + 0.7071068e31
r5 * D * ~r5= (1.1102230246251565e-16, -0.5, 0.8660254037844387)
D1= (0.9501662436948253, -0.09307454871392543, 0.2975251883867395)
D2= (0.8059644942642701, -0.20116805856524245, 0.5567339096897463)
D3= (0.5827297382221729, -0.31278543658629104, 0.750060879429824)
D4= (0.3042016457656299, -0.41605684767852313, 0.8569469401388232)
D5= (5.551115123125783e-17, -0.5, 0.8660254037844382)
def Root(R_,n): # n-th root of rotor R
R=R_.normalized()
LogR_n=Log®(1.0/n)
x2= LogR_n | LogR_n
x2 = x2.mvec[0]
ha = math.sqrt(-x2) # x2 must be negative
I= -1LogR_n*(1.0/ha) # watch for div by 0
return math.cos(ha)-math.sin(ha)*I