I come from a background of screw theory for rigid body mechanics and was pleasantly surprised when I discovered PGA as it addresses a lot of my gripes and inconsistencies.
Anyway, in my thesis I stated that twists (motors) and wrenches (forques) are lines in Plucker coordinates plus a pitch and magnitude.
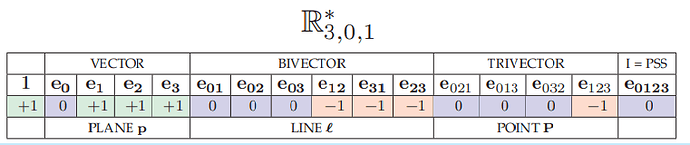
Lines in 3D PGA are the following basis vectors
So for example,
- To encode a force \vec{F}=(F_x,F_y,F_z) you would use {\bf f} =F_z{\bf e}_{12}+F_y{\bf e}_{31}+F_x{\bf e}_{23}
- To encode a torque \vec{\tau}=(\tau_x,\tau_y,\tau_z) you would use {\bf f} =\tau_x{\bf e}_{01}+\tau_y{\bf e}_{02}+\tau_z{\bf e}_{03}
The way these are ordered in code would be
f = [0, 0,0,0, τx,τy,τz,Fz,Fy,Fx, 0,0,0,0, 0]
I wish the ordering would be different such as the familiar cadence of (x,y,z) is maintained, and each basis vector would be the same sequence as its dual vector.
\star\begin{pmatrix}{\bf e}_{01} & {\bf e}_{02} & {\bf e}_{03}\end{pmatrix}=\begin{pmatrix}{\bf e}_{23} & {\bf e}_{31} & {\bf e}_{12}\end{pmatrix}
\star\begin{pmatrix}{\bf e}_{1} & {\bf e}_{2} & {\bf e}_{3}\end{pmatrix}=\begin{pmatrix}{\bf e}_{032} & {\bf e}_{013} & {\bf e}_{021}\end{pmatrix}
and vice-versa.
a similar problem exists for encoding the point (x,y,z)
P=[0, 0,0,0, 0,0,0,0,0,0, z,y,x,1, 0]
This can be achieved with the following ordering:
Before:
\begin{array}{ccccc} \underbrace{1}_{\text{scalar}} & \underbrace{\left(\begin{array}{c|ccc} {\bf e}_{0} & {\bf e}_{1} & {\bf e}_{2} & {\bf e}_{3}\end{array}\right)}_{\text{vector(plane)}} & \underbrace{\left\{ \begin{array}{ccc|ccc} {\bf e}_{01} & {\bf e}_{02} & {\bf e}_{03} & {\bf e}_{12} & {\bf e}_{31} & {\bf e}_{23}\end{array}\right\} }_{\text{bivector(line)}} & \underbrace{\left[\begin{array}{ccc|c} {\bf e}_{021} & {\bf e}_{013} & {\bf e}_{032} & {\bf e}_{123}\end{array}\right]}_{\text{trivector(point)}} & \underbrace{{\bf e}_{0123}}_{\text{pseudo-scalar}}\end{array}
After:
\begin{array}{ccccc} \underbrace{1}_{\text{scalar}} & \underbrace{\left(\begin{array}{c|ccc} {\bf e}_{0} & {\bf e}_{1} & {\bf e}_{2} & {\bf e}_{3}\end{array}\right)}_{\text{vector(plane)}} & \underbrace{\left\{ \begin{array}{ccc|ccc} {\bf e}_{01} & {\bf e}_{02} & {\bf e}_{03} & {\bf e}_{23} & {\bf e}_{31} & {\bf e}_{12}\end{array}\right\} }_{\text{bivector(line)}} & \underbrace{\left[\begin{array}{ccc|c} {\bf e}_{032} & {\bf e}_{013} & {\bf e}_{021} & {\bf e}_{123}\end{array}\right]}_{\text{trivector(point)}} & \underbrace{{\bf e}_{0123}}_{\text{pseudo-scalar}}\end{array}
Now the dual() operator should be easier as no re-ordering of coefficients is needed (going from point to plane for example). As you can see below the Hodge dual operator should maintain the same cadence.
Or am I wrong in the interpretation of how to encode the familiar line and axial vectors as bivectors?
PS. The Cayley Table should now contain the familiar wedge/cross-product operator matrix \begin{bmatrix}0 & -v_{z} & v_{y}\\ v_{z} & 0 & -v_{x}\\ -v_{y} & v_{x} & 0 \end{bmatrix}