The user Ravensburg recently posted on the discord GA channel the following question:
I’m looking at the feasibility of using projective transformations to deform a unit cube into an arbitrary (convex) hexahedron where each vertex of the cube is mapped to a vertex of the hexahedron …
I’m posting an answer to his question here (rather than on discord) because I find the theme-based organization on this forum preferable for my old brain to be able to find old posts and keep conversations focused. (I’ll also post a link to this post onto discord.)
This is a very interesting question. It can serve as a good introduction to projective transformations in 3D. The short answer is that with projective transformations you will get most but not all possible hexahedrons. There is an 18-dimensional family of hexahedrons, projective transforming a cube produces a 15-dimensional sub-family. This sub-family can be described by the following property:
P1: The intersection lines of opposite faces of the hexahedron lie in a plane
P1 is certainly satisfied by a cube: opposite faces are parallel, so the intersection lines are ideal, and so lie in the ideal plane. We want to show now that a hexahedron C' satisfies P1 \Leftrightarrow there exists a projective transformation H such that H(C) = C'.
First a couple of properties of projective transformations in n-D:
T1. A projective transformation is determined by the image of (n+2) linearly independent points.
T2. A projective transformation preserves incidence. If two points are joined by the line then the image of the two points will be joined by the image of the line, etc.
T3. Every projective transformation can be represented by an invertible (n+1) x (n+1) matrix M, where \lambda M represents the same projective transformation when \lambda \neq 0. That is, a projective transformation of \mathbb{R}P^n is an element of PGL(\mathbb{R},n+1), the projectivized group of invertible linear maps of \mathbb{R}^{n+1}. This is a group with dimension (n+1)^2-1 = n(n+2). The latter number coincides with the number of ways to choose (n+2) n-dimensional points, so T1 and T3 are consistent in regard to the number of projective transformations.
T4. We’ll consider here only collineations, that is, projective transformations that map points to points; a correlation is a projective transformation that maps points to planes and vice-versa. (The same matrix M can be interpreted as both a collineation and a correlation).
(\Leftarrow): Let \mathbf{e}_0 be the ideal plane. Since intersections of opposite face-planes of C lie in \mathbf{e}_0, T2 implies the opposite face-planes of H(C) will lie in H(\mathbf{e}_0).
(\Rightarrow): Given C' we’ll construct a projective transformation H such that H(C) = C'.
We don’t need PGA to solve this problem since it’s not a metric question but it’s helpful to use the notation available. Let \{\mathbf{E}_0, \mathbf{E}_1, \mathbf{E}_2, \mathbf{E}_3 \} be the standard basis for euclidean 3-space. Then \mathbf{E}_0 is the origin and \mathbf{E}_1 is the ideal point in the x-direction, etc. Define \mathbf{E}_4 := \mathbf{E}_0 + \mathbf{E}_1 + \mathbf{E}_2 + \mathbf{E}_3. This is sometimes called the unit point in classical projective geometry. Notice that we have now altogether 5 points (exactly enough to specify a projective transformation in 3 dimensions.)
Reconstruction C from \{\mathbf{E}_i\}
Let C be the cube with opposite vertices \mathbf{E}_0 and \mathbf{E}_4. The face-planes of the cube passing through \mathbf{E}_0 are then given by
\mathbf{p}_{x-} := \mathbf{E}_0\vee \mathbf{E}_2 \vee \mathbf{E}_3,
\mathbf{p}_{y-} :=\mathbf{E}_0\vee \mathbf{E}_3 \vee \mathbf{E}_1,
\mathbf{p}_{z-} :=\mathbf{E}_0\vee \mathbf{E}_1 \vee \mathbf{E}_2
(the x=0, y=0, and z=0 planes),
while the planes through \mathbf{E}_4 are given by
\mathbf{p}_{x+} := \mathbf{E}_4\vee \mathbf{E}_2 \vee \mathbf{E}_3,
\mathbf{p}_{y+}:= \mathbf{E}_4\vee \mathbf{E}_3 \vee \mathbf{E}_1,
\mathbf{p}_{z+} :=\mathbf{E}_4\vee \mathbf{E}_1 \vee \mathbf{E}_2
(the x=1, y=1, and z=1 planes).
Then the other vertices of the cube can be calculated by intersecting these planes. For example, the corner (1,0,1,1) is the intersection
\mathbf{V}_{+-+} = \mathbf{p}_{x+} \wedge \mathbf{p}_{y-} \wedge \mathbf{p}_{z+}, etc.
Defining the projectivity H
Now we want to show how if we have any hexahedron C' satisfying property P1 then we can find a unique projective transformation such that H(C) = C'.
Let \mathbf{F}_0 and \mathbf{F}_4 be a pair of opposite vertices of C'.
Let \mathbf{\ell}_i \text{, for } i \in \{1,2,3\}, be the intersection lines of opposite sides of C' .
Let \mathbf{F}_i := \mathbf{\ell}_j \wedge \mathbf{\ell}_k \text{, for } i \in \{1,2,3\}, be the pair-wise intersections of these lines (these intersections exist by property P1).
Claim: The projectivity H determined by H(\mathbf{E}_i) = \mathbf{F}_i satisfies H(C) = C'.
Proof: It’s an easy exercise to show that the faces and vertices of C' are the images of the faces and vertices of C using T2, the incidence invariance of projective maps.
Computing the matrix of H
We sketch here how to construct the matrix for the projectivity H such that H(\mathbf{E}_i) = \mathbf{F}_i.
This is a general technique that I’m including here because it’s not so well known and it’s a useful piece of knowledge.
The matrix is with respect to the basis \{\mathbf{E}_0, \mathbf{E}_1, \mathbf{E}_2, \mathbf{E}_3 \}.
Let M := (\mathbf{F}_0, \mathbf{F}_1, \mathbf{F}_2, \mathbf{F}_3) be the matrix whose columns are the given points. Then M\mathbf{E}_i = \mathbf{F}_i, i\in\{0,1,2,3\} . We find a non-zero weight vector \mathbf{\lambda} := \{\lambda_0,\lambda_1,\lambda_2,\lambda_3\} such that M\lambda = \mathbf{F}_4. This is obtained by \lambda := M^{-1}\mathbf{F}_4.
Then define M_H = (\lambda_0 \mathbf{F}_0, \lambda_1 \mathbf{F}_1,\lambda_2 \mathbf{F}_2, \lambda_3 \mathbf{F}_3).
M_H satisfies M_H\mathbf{E}_i = \lambda_i \mathbf{F}_i \cong \mathbf{F}_i where \cong denotes projective equivalence. Finally, M_H \mathbf{E}_4 = M \lambda = \mathbf{F}_4.
This completes the construction.
[The basic idea is to get a first guess that maps the first four source points to the first four target points, and then to add in the fifth pair by adjusting the projective weights of the first four target points so that their sum yields the fifth target point.]
Remarks:
-
Dimension-counting The space of hexahedra is 18-dimensional since you can freely deform any of the six face planes of the cube and still maintain the topology of the cube (6 quadrilaterals meeting 3 at each of 8 vertices). Each plane depends on 3 parameters, giving 6x3=18. The space of hexahedra is 15-dimensional since there is a 1:1 map to the projective group in 3 dimensions, which has 3x5=15 dimensions. You can also confirm that the condition that the intersection lines of opposite faces lie in a single plane reduces the dimension by 3: each pair of such lines must intersect. (The space of lines is 4D, the space of lines meeting a given line is 3D, a reduction of 1 degree of freedom).
-
Comparison to 2D The situation is 2D gives no hint of the situation in 3D since in 2D you can construct the projective transformation by mapping the four corners of the square to any arbitrary four points (property T1 in 2D), or 4 edge lines of the square to any four lines. In 3D however the cube has 8 vertices which is too many to map projectively. Looking instead at the face planes is better since there are only six, but it’s still one too many to construct a projective transformation.
-
The Reyes configuration The configuration described above for the cube includes 11 points, 12 lines, and 6 planes. If we include the 6 planes obtained by joining the opposite edges of the cube and their common intersection point (the center of the cube) and their pair-wise intersection lines (the four space diagonals of the cube ), this produces a configuration of 12 vertices, 16 lines and 12 planes. It’s a completely symmetric configuration: through each point go 6 planes and 4 lines; on each line lie 3 points and pass 3 planes; and in each plane lie 6 points and 4 lines. Any of the points can serve as the “center” of the hexahedron; then the 8 adjacent points form the set of vertices, the six planes not incident with the “center” form the face-planes, and the other three vertices are the intersections of the “opposite” face planes.
Consequently, there is a group of 576 projective transformations that map this hexahedron to itself (12 times the 48 “symmetries of a cube” that fix a given vertex). I could go on … 
It’s called the Reyes configuration and you can read more about it here.
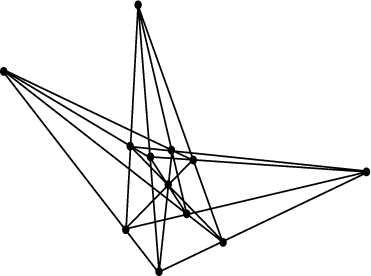
Image from Wolfram MathWorld.
You can see an application of such “projective hexahedra” in this video on the Schatz linkage and the oloid surface. The relevant section starts at 1:41 in the video.