How does a Plucker’s coordinate for line works in PGA? Is it e01,e02,e03 for direction and e23,e31,e12 to specify a point located on that line, or is it the wedge product (Point ^ line) ? Does the direction have to be normalized?
My goal was in fact to draw a line, aiming in a specific direction , passing
through a specific point (knowing the Plucker’s line was a way to do that)…Here is the solution, I was looking for:
var dir = (x,y,z)=>!(x1e1 + y1e2 + z1e3);
var point = (x,y,z)=>!(1e0 + x1e1 + y1e2 + z1e3);
var Pt = point(-0.5,0.5,1)
var u = dir(1,1,1)
var L = (Pt&u)
Hi @charpelletier,
That’s certainly a valid solution. More generally the PGA form of the Plucker condition is simply L \wedge L = 0. There are plenty of ways to generate valid Plucker lines:
- The wedge of any two planes a,b produces a Plucker line at their intersection : L = a \wedge b
- The join of any two Euclidean points p_1,p_2 produces a Plucker line through them : L = p_1 \vee p_2
- The join of a Euclidean point p_1 and an infinite point (direction) p_\infty also does : L = p_1 \vee p_\infty
- The inner product between a point p and a plane a produces a line through the point, \perp to the plane : L = a \cdot p
And probably some more I’m forgetting 
Thank you.
In fact, I am still looking for a proper understanding of the Plucker line coordinate. I was trying to trace a line from the formula itself(see below), by entering the direction components and the moment components. Even though the direction components seem obvious, I can’t grasp the geometric meaning of the moment components!!
/*
Pt = (a,b,c) // any Point on the line
u = (u,v,w) // line direction
L = (u1e23 - v1e13 + w*1e12) + ( (av-bu)*1e03 -(aw-cu)*1e02 +(bw-cv)*1e01) // tested ok
// L = (“direction”) + ( " moment" ) // derived from !(Pt & u) = (!Pt ^ !u)
*/
Here’s a bit of geometry that may help to understand what the Pluecker coordinates mean. The main idea is to write a given line as the sum of a line through the origin and an ideal line. Each of these parts contains important information from which you can completely describe the original line.
Given a line L := a_{01}e_{01} + a_{02}e_{02}+a_{03}e_{03}+ a_{12}e_{12}+a_{31}e_{31}+ a_{23}e_{23}.
Write L as the sum of two lines L = L_o + L_\infty:
L_o := a_{12}e_{12}+a_{31}e_{31}+ a_{23}e_{23} and
L_\infty = a_{01}e_{01} + a_{02}e_{02}+a_{03}e_{03}
Set-up
- The “Pluecker condition” that a bivector L is a line is a_{01}a_{23} + a_{02} a_{31} + a_{03}a_{12} = 0.
- For what follows it’s useful to define \{E_1,E_2,E_3\} := \{e_{032},e_{013},e_{021}\}, the x-, y-, and z- coordinate directions (ideal points).
- Also recall that the orthogonal complement \mathbf{X}^\perp := \mathbf{XI} where \mathbf{I} is the unit pseudoscalar.
Exercise:
- L_o is a line through the origin.
- The ideal point of L_o (and L) is \mathbf{V} := a_{23}E_1 + a_{31}E_2+ a_{12}E_3. [Notice the reversal of order in the triple of Pluecker coordinates!]
- L_\infty is an ideal line that passes through \mathbf{V} hence meets L. This is equivalent to the Pluecker condition on the coordinates as can be seen by computing L_\infty \vee \mathbf{V}.
- Since L_o and L_\infty have a common point V, any linear combination aL_o + bL_\infty will also pass through V. The set of such lines is called the line pencil spanned by L_o and L_\infty. In particular L = L_o + L_\infty belongs to this pencil (for a=1,b=1).
- L is obtained from L_o by translating it parallel to itself in the plane L\wedge L_\infty, a distance equal to \|L\|_\infty. (As we learn in euclidean PGA, this translation can be thought of as “rotation” in the plane L\wedge L_\infty around the ideal point \mathbf{V}.)
- The ideal point \mathbf{T} := a_{01}E_1 + a_{02}E_2 + a_{03}E_3 is the “pole” of the ideal line L_\infty (i. e., is at right angles to all the points of L_\infty).
- \mathbf{T} = (L_\infty \vee \mathbf{P})^\perp for any euclidean normalized euclidean point \mathbf{P}.
- The Pluecker condition, in older texts, is expressed by the condition that \mathbf{T} and \mathbf{V} are perpendicular vectors, i. e., a_{01}a_{23} + a_{02} a_{31} + a_{03}a_{12} = 0.
- The direction of the translation L_o+L_\infty is (L \vee \mathbf{T})^\perp, the direction normal to the plane spanned by L and \mathbf{T}.
- Carry out the above analysis for the line L = e_{03} - d E_{31}.
Remark: This leads us to a nice generalization of a well-known fact from ordinary vector algebra:
For a euclidean point P and an ideal point V , P \rightarrow P + V translates P by V. The distance moved equals \|V\|_\infty.
Our new result is:
For a euclidean line L and an ideal line M (satisfying L \wedge M= 0), L \rightarrow L + M translates L by M. The distance moved equals \|M\|_\infty.
Exercise: deduce a similar result for translating euclidean planes.
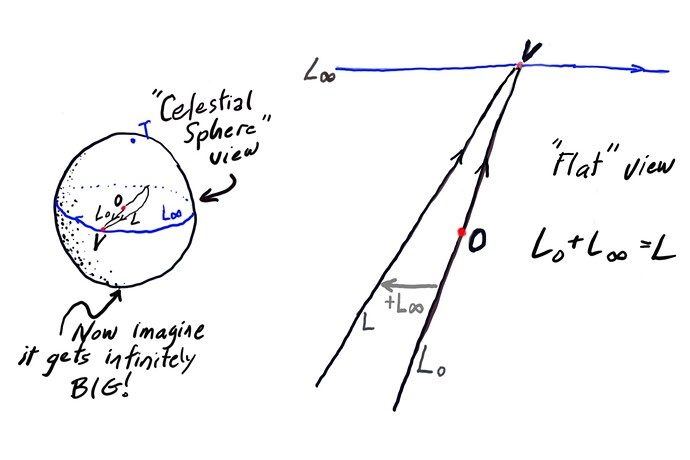
The following sketch attempts to picture the decomposition L = L_o + L_\infty described in my previous post.
The right view is the more traditional one, but in perspective so \mathbf{V} is visible.
The left view focus on the plane at infinity, picturing it as a very big sphere. It allowed me to include the vector \mathbf{T}, the “pole” of L_\infty. The reader/viewer should imagine that the sphere continues to grow until it is flat.
Thank you, that is very helpful.
I am right to say that when L is obtained from L=a L_o + b L_\infty, then all L’s(pink lines) are part of the same line pencil (located on plane: L_o ^ L_\infty) , but if we translate L_o to L, the way shown below (red lines), then L becomes part of another line pencil? I still struggle on the way to translate L_o to the exact same L with a rotation (L2 green).
//++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
var a23=1, //u direction through the origine
a31=1, //v
a12=0 //w
//++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
var V = a231e032+a311e013+a12*1e021 // The ideal point of Lo
//++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
//++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
var Lo = (1e123 & V) // Line: Pt & dir
//++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
//++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
var sqrt = motor => (Math.sign(motor.s) + motor).Normalized;
var motor = (line,angle_or_distance)=>Math.E**(angle_or_distance/2 * line);
//++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
//++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
var here = point(1,0,1)
var Trans = ()=>sqrt(1e123 * here)
var Rotat = motor(Lo,here/2) //----------<<<<<--------------
var L = ~Trans * Lo * Trans
var L2 = ~Rotat * Lo * Rotat
//++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
@charpelletier
I just noticed your post from a year ago.
I’ve reread it twice and I still can’t say that I understand the figure. What role does the green line play?
You can only translate a line onto another line when the two lines are parallel. Then the line that you have to add to carry out the translation is the ideal line of the pencil determined by the two parallel lines.