Papers / books / notes on numerical stability for 2D PGA with FPUs?

[julialongtin]

I’ve been doing property testing on my haskell projective geometric algebra library. this tests my engine, and finds cases where properties are not true.

I’ve been writing this problem up, and asking for opinions in side channels, but thought i might ask here: has anyone done any work on numeric stability with a PGA system, using floating point math, just generally?

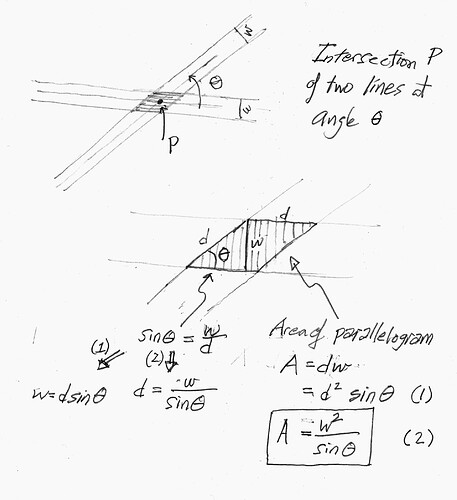
At the moment, I am trying to determine how big a circle i have to draw around the intersection of two lines, to guarantee that the real answer is somewhere in the circle.

I’m going to paste my current writeup below, but i would accept any answers people have to give about error drift with a 2D PGA system implemented in doubles. I’ve done a lot of work in this area, but think i’ve got the issue cornered in my program enough to start requestion outside help. I’m using ULP tracking at every operation, and trying to create a “what is the maximum amount off this value is” function, so i can reason about error, rather than ignore it.

Thanks everyone.

Julia Longtin

----- SNIP -----

Problem description:

We use floating point calculations. When we intersect two lines, the point that is returned is not exactly where it would be in a non-floating point world.

To try and resolve this, we’ve done ULP tracking of all of the input calculations, and have a function that transforms a loss value (“what was lost at each calculation”) to an estimated error (“what is the maximum distance from reality for this result”). This lets us define a circle around our calculated point, and guarantee the real point is within that circle.

Ideally, when we intersect two lines, we should get a point, and an error radius defining a circle around the point, such that the real, ideal world point would be guaranteed to be within said circle. With the current code, that error calculation gives the wrong value and the circle ends up too small.

We have verified that we correctly preserve all of the loss values at each calculation step, but the transformation of that loss into an error radius is incorrect. bonus: the amount of imprecision goes up as really steep angles (near 180 degrees) get involved.

What we need is a modification of the error calculation function so it correctly calculates the error circle. We can verify that this was done by making sure the tests described below all pass.

The Branch:

GitHub - Haskell-Things/HSlice at fix_distanceBetweenNPLine2sWithErr

(yes, this is badly named, with a bad commit history)

The test:

./dist-newstyle/build/x86_64-linux/ghc-9.0.2/hslice-0.0.1/t/test-hslice/build/test-hslice/test-hslice -a 10000 --match "/Contour facetization algorithms/Arcs (Skeleton/Concave)/finds that all motorcycles intersect at the same point in a triangle/"

This test generates random triangles. It takes the bisector of each angle of the triangle, and then calculates the points and error circles for each pair of bisector intersections. Ideally, those intersections should be the same point. Due to floating point error, they are not, but the distance between them should be less than or equal to the sum of their error distances. However, the test will sometimes find triangles where this is not the case.

When the test fails, it dumps a section of code that you can drop into the online Projective Geometric Algebra viewer, complete with some of the associated haskell structures in comments. for example:
https://enkimute.github.io/ganja.js/examples/coffeeshop.html#bf5qID6Vx

the variables d, e, and f, contain the three points that are found. After their declarations, we have dumped the error-component of all of the operations, AND the angle (as SIN). note that all of the error cases contain one intersection with an angle that is -0.99999… so, “really steep”, and the - means “toward each other”. The point corresponding to this really steep intersection is quite far from the other two points, and it’s error circle has no space in common with the error circles of the other two intersections points.

The Test’s code:

The test is at:
HSlice/PGA.hs at fix_distanceBetweenNPLine2sWithErr · Haskell-Things/HSlice · GitHub
… but i don’t think that’s very useful. the actual point-distance-checking function is
HSlice/Intersections.hs at fix_distanceBetweenNPLine2sWithErr · Haskell-Things/HSlice · GitHub

to make this almost never fail, i have added a fudge factor to HSlice/PGA.hs at fix_distanceBetweenNPLine2sWithErr · Haskell-Things/HSlice · GitHub

The pPointFuzziness function is responsible for looking at all of the error when a point was created, and determining the maximum imprecision, or how far to draw a circle around this point, and guarantee that the real answer is within that circle. The 10000 in line 276 is completely made up, and does a really good job of solving this for a LOT of cases. Obviously, this should be replaced with a function. All of the potential inputs to that potential function are available inside of pPointFuzziness.

using a ‘1’ in place of the ‘10000’ results in a failing case within approximately random 250 tests. 10,000 gets us a few tens of thousands of tests before it can generate a skinny enough triangle to trigger the bug.

[julialongtin]

I haven’t made any progress on this, but i have done the work to get 20,000 results of this, along with all of the error values, and the idealNorm of the intersections into a spreadsheet. this has changed a few of the line numbers in the above links, unfortunately.

I have exported all of this into a CSV file you can download at https://faikvm.com/testrun.csv

If anyone needs information about what these fields are, i’m available to explain, and would really appreciate the assistance.

Thank you!

Julia Longtin

[julialongtin]

just so anyone following along knows my current thought process… i can now generate training sets, so might see if i can, with the help of another haskeller, force a neural net to at least tell me what components are important, and see if it can be trained to do the job. the second thought that’s percolating in my brain is: what i’m really looking at is the difference between where my program thinks pairs of lines are collinear (the ideal norm is less than the error generated by checking what the ideal norm is), and where they have a definable intersection point. hense, i included the ideal norm in the above spreadsheet.

Ideas are certainly welcome.

[cgunn3]

Hi @julialongtin!
I venture a reply although I have not had time to investigate the online resources you have created.
I offer some general remarks about the intersection of two lines that may or may not be relevant here.

The fact that we are using floating point values for lines means, roughly speaking, that each line, instead of being an infinitely thin object, has a fuzzy outline. For the purposes of approximation we can think of it as a thin strip, whose width w is the limit of precision of your floating point values. Points that lie on the (exact) line are guaranteed to lie within this strip, but otherwise you don’t know exactly where the points of the lines are. (It’s a bit more complicated than this but I think it’s close enough to make sense of the following argument.)

If the lines are exact, then the intersection point is exact. Otherwise, the intersection point has to lie within the intersection of the fuzzy strips corresponding to the lines. The smaller the angle, the larger the area of the overlap of the two strips. Consult the following figure:

To be exact, the area of the overlap is the area A of the parallelogram with base d and height w. Using the relation \sin{\theta} = \dfrac{w}{d} yields two formulas for the area A. (1) on the right is the traditional formula for the area A of a parallelogram in terms of the side length d while (2) gives the formula we need in terms of the constant w, the width of the fuzzy strips.

Summing up: the area of this intersection is proportional to the inverse of the sine of the angle between the lines: the smaller the angle, the greater the uncertainty where the intersection point is \Rightarrow loss of precision.

For small angles, \sin{\theta} \sim \theta, which implies that the precision decreases linearly with the angle, for small angles. Applied to the circles that should contain the computed intersection points:
each time you divide the angle between the lines by a factor s, the circle should increase its radius by the same factor s.

Notice that none of the above reasoning applies specifically to geometric algebra or PGA in particular. Everything said above applies in traditional approaches to calculating intersections of lines using linear equations/determinants. I expect that a good book on numerical methods would provide insight into the behavior you are observing.

The following graph also shows a simple Mathematica experiment I ran using double-precision arithmetic, to calculate the intersection point of two lines separated by an angle \theta. I can post the details of the code if anyone is interested.

The vertical axis v represents the number of digits of precision that were lost in the calculation: v = log_{10}(\|P_x - P_c\|_\infty) the base-10 log of the euclidean norm of the vector between the exact and the calculated intersection point).

The horizontal axis variable h can be converted to the angle \theta by the formula \theta = 10^{-.1h}., so the graph is in effect a log - log graph.

Note that when the lines are parallel, the calculation yields a definite point – but an ideal, not a euclidean point. This ideal point can be thought of as a vector, the direction common to both points. The ideal norm of this result is the euclidean distance between the two lines!

I don’t have any magic solution to the loss of precision you’ve observed. My impression is that the angles that might cause serious problems are so small that they don’t tend to arise in practical applications. After all, in the above example, the precision remains within 8 digits as long as the angle exceeds 10^{-7} radians! Of course these exponents have to be halved for floating point precision.

[jrus]

Have you searched about exact computation and geometric robustness more generally? (not w/r/t PGA in particular?)

For instance starting with
https://www.cs.cmu.edu/~quake/robust.html
https://cs.nyu.edu/exact/papers/
https://www.cgal.org