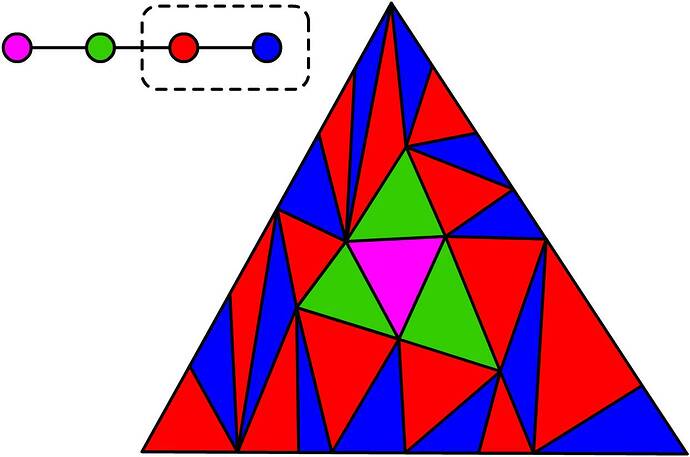
Hi there! The tiling problem below is relevant to my logic thesis. Do you have any idea on how to tackle it? Or can you refer me to people who might be able to help?
A triangle tiling is a finite set \mathcal{T}\subseteq\mathcal{P}(\mathbb{R}^2) of triangles such that
- \cup\mathcal{T} is a triangle;
- for any T,T'\in\mathcal{T} we either have
- T\cap T'=\emptyset,
- T\cap T'=\{v\} for some point v that is a corner vertex of both T and T',
- T\cap T' is a full edge of both T and T', or
- T=T'.
Equivalently, \mathcal{T} is a triangle tiling iff there exists a twodimensional simplicial complex \Sigma\subseteq\mathcal{P}(\mathbb{R}^2) such that the carrier of \Sigma is a triangle and \mathcal{T} is the set of triangles in \Sigma.
Suppose that G=(V,E) is a finite undirected graph and B\subseteq V.
We say that a triangle tiling \mathcal{T} is (G,B)-colored by a map f:\mathcal{T}\rightarrow V if
- for any T,T'\in\mathcal{T} such that T\cap T' is an edge of T and T', we have \big\{f(T),f(T')\big\}\in E;
- for any T\in\mathcal{T} we have f(T)\in B iff T intersects the boundary of \cup\mathcal{T};
- f is surjective.
We wonder whether the following problem is decidable: given a finite undirected graph G=(V,E) and B\subseteq V, is there a triangle tiling \mathcal{T} that can be (G,B)-colored?
The picture exemplifies this problem with an instance for which the answer is ``yes’'.