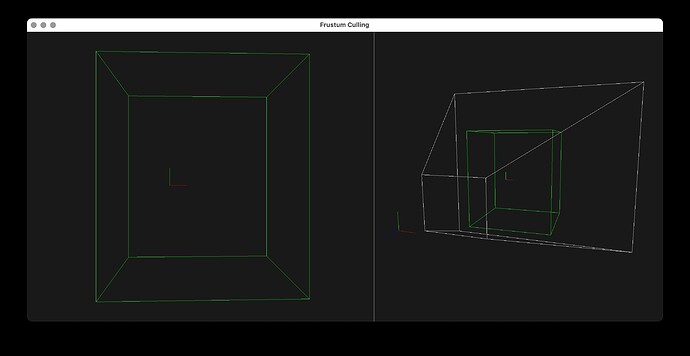
Here is the source code to my desktop test application. I am running it on macOS 11.5.2, using glfw and glm from homebrew. The main file might have to be modified a bit on other platforms to get OpenGL running (I’m using version 2.1)
Note that the code is not optimized at all. I just wanted to get the algorithm implemented (hopefully) correctly.
frustum_culling.cpp
#include <GLFW/glfw3.h>
#include <glm/glm.hpp>
#include <glm/ext.hpp>
#include <glm/gtx/quaternion.hpp>
#include <cmath>
#include <vector>
#include <iostream>
struct AABB
{
glm::vec3 min;
glm::vec3 max;
};
struct Viewport
{
float x, y, width, height;
};
// https://discourse.bivector.net/t/frustum-culling-in-ga/430
std::vector<bool> intersectFrustum(const glm::mat4x4& view_projection, const std::vector<AABB>& aabbs)
{
// http://donw.io/post/frustum-point-extraction
PGA3D frustum_points[8];
{
glm::mat4x4 clip_to_world = glm::inverse(view_projection);
// near == [0 1 2 3]
// far == [4 5 6 7]
// origin at [0 0 0]
//
// 7----6 y
// /| /| ^
// 3----2 | |
// | 4--|-5 o--> x
// |/ |/ /
// 0----1 z
glm::vec4 frustum[8] =
{
{-1, -1, -1, 1}, // 0
{ 1, -1, -1, 1}, // 1
{ 1, 1, -1, 1}, // 2
{-1, 1, -1, 1}, // 3
{-1, -1, 1, 1}, // 4
{ 1, -1, 1, 1}, // 5
{ 1, 1, 1, 1}, // 6
{-1, 1, 1, 1} // 7
};
for (int i = 0; i < 8; i++)
{
frustum[i] = clip_to_world * frustum[i];
frustum[i] /= frustum[i].w;
frustum_points[i] = point(frustum[i].x, frustum[i].y, frustum[i].z);
}
}
// I constructed the planes such that frustum_planes[i] v mid_point < 0
//
// Another option to define the planes, but I need the frustum_points anyways
// https://fgiesen.wordpress.com/2012/08/31/frustum-planes-from-the-projection-matrix
PGA3D frustum_planes[6];
{
frustum_planes[0] = (frustum_points[0] & frustum_points[3] & frustum_points[7]).normalized(); // left
frustum_planes[1] = (frustum_points[1] & frustum_points[5] & frustum_points[6]).normalized(); // right
frustum_planes[2] = (frustum_points[0] & frustum_points[4] & frustum_points[5]).normalized(); // bottom
frustum_planes[3] = (frustum_points[2] & frustum_points[6] & frustum_points[7]).normalized(); // top
frustum_planes[4] = (frustum_points[0] & frustum_points[1] & frustum_points[2]).normalized(); // near
frustum_planes[5] = (frustum_points[4] & frustum_points[7] & frustum_points[6]).normalized(); // far
// TODO: This should be done both for the planes and lines
//// Extend frustum around mid_point to avoid numerical problems on the boundary
//for (int i = 0; i < 6; ++i)
//{
// frustum_planes[i][A0] += 0.01;
//}
}
// Edge lines of the frustum
PGA3D f_mn[6][4];
{
// left
f_mn[0][0] = frustum_points[0] & frustum_points[3];
f_mn[0][1] = frustum_points[3] & frustum_points[7];
f_mn[0][2] = frustum_points[7] & frustum_points[4];
f_mn[0][3] = frustum_points[4] & frustum_points[0];
// right
f_mn[1][0] = frustum_points[1] & frustum_points[5];
f_mn[1][1] = frustum_points[5] & frustum_points[6];
f_mn[1][2] = frustum_points[6] & frustum_points[2];
f_mn[1][3] = frustum_points[2] & frustum_points[1];
// bottom
f_mn[2][0] = frustum_points[0] & frustum_points[4];
f_mn[2][1] = frustum_points[4] & frustum_points[5];
f_mn[2][2] = frustum_points[5] & frustum_points[1];
f_mn[2][3] = frustum_points[1] & frustum_points[0];
// top
f_mn[3][0] = frustum_points[2] & frustum_points[6];
f_mn[3][1] = frustum_points[6] & frustum_points[7];
f_mn[3][2] = frustum_points[7] & frustum_points[3];
f_mn[3][3] = frustum_points[3] & frustum_points[2];
// near
f_mn[4][0] = frustum_points[0] & frustum_points[1];
f_mn[4][1] = frustum_points[1] & frustum_points[2];
f_mn[4][2] = frustum_points[2] & frustum_points[3];
f_mn[4][3] = frustum_points[3] & frustum_points[0];
// far
f_mn[5][0] = frustum_points[4] & frustum_points[7];
f_mn[5][1] = frustum_points[7] & frustum_points[6];
f_mn[5][2] = frustum_points[6] & frustum_points[5];
f_mn[5][3] = frustum_points[5] & frustum_points[4];
}
// Edge indices of the AABB
glm::ivec2 e_jk[12];
{
e_jk[0] = glm::ivec2(0, 1);
e_jk[1] = glm::ivec2(1, 2);
e_jk[2] = glm::ivec2(2, 3);
e_jk[3] = glm::ivec2(3, 0);
e_jk[4] = glm::ivec2(4, 5);
e_jk[5] = glm::ivec2(5, 6);
e_jk[6] = glm::ivec2(6, 7);
e_jk[7] = glm::ivec2(7, 4);
e_jk[8] = glm::ivec2(0, 4);
e_jk[9] = glm::ivec2(1, 5);
e_jk[10] = glm::ivec2(2, 6);
e_jk[11] = glm::ivec2(3, 7);
}
float d_ij[6][8];
PGA3D aabb_points[8];
const auto intersect = [&frustum_planes, &f_mn, &e_jk, &d_ij, &aabb_points](const AABB& aabb)
{
aabb_points[0] = point(aabb.min.x, aabb.min.y, aabb.min.z).normalized();
aabb_points[1] = point(aabb.max.x, aabb.min.y, aabb.min.z).normalized();
aabb_points[2] = point(aabb.max.x, aabb.max.y, aabb.min.z).normalized();
aabb_points[3] = point(aabb.min.x, aabb.max.y, aabb.min.z).normalized();
aabb_points[4] = point(aabb.min.x, aabb.min.y, aabb.max.z).normalized();
aabb_points[5] = point(aabb.max.x, aabb.min.y, aabb.max.z).normalized();
aabb_points[6] = point(aabb.max.x, aabb.max.y, aabb.max.z).normalized();
aabb_points[7] = point(aabb.min.x, aabb.max.y, aabb.max.z).normalized();
// Check if any aabb point is inside the frustum
for (int j = 0; j < 8; ++j)
{
const PGA3D& P_j = aabb_points[j];
d_ij[0][j] = (frustum_planes[0] & P_j)[AO];
d_ij[1][j] = (frustum_planes[1] & P_j)[AO];
d_ij[2][j] = (frustum_planes[2] & P_j)[AO];
d_ij[3][j] = (frustum_planes[3] & P_j)[AO];
d_ij[4][j] = (frustum_planes[4] & P_j)[AO];
d_ij[5][j] = (frustum_planes[5] & P_j)[AO];
if (d_ij[0][j] < 0 && d_ij[1][j] < 0 && d_ij[2][j] < 0 && d_ij[3][j] < 0 && d_ij[4][j] < 0 && d_ij[5][j] < 0)
{
return true;
}
}
// Check if any aabb edge intersects any of the frustum faces
for (int i = 0; i < 6; ++i) // frustum face
{
for (const glm::ivec2& e : e_jk) // edges
{
if (d_ij[i][e.x] * d_ij[i][e.y] < 0) // edge points on opposite sides of the face
{
PGA3D x_jk = (aabb_points[e.x] & aabb_points[e.y]); // edge line
const float e0 = (f_mn[i][0] & x_jk)[AO];
const float e1 = (f_mn[i][1] & x_jk)[AO];
const float e2 = (f_mn[i][2] & x_jk)[AO];
const float e3 = (f_mn[i][3] & x_jk)[AO];
if (e0 != 0 && e1 != 0 && e2 != 0 && e3 != 0)
{
const bool sb = std::signbit(e0);
if (std::signbit(e1) == sb && std::signbit(e2) == sb && std::signbit(e3) == sb)
{
return true;
}
}
}
}
}
return false;
};
std::vector<bool> intersecting(aabbs.size());
for (int aabb_id = 0; aabb_id < aabbs.size(); ++aabb_id)
{
intersecting[aabb_id] = intersect(aabbs[aabb_id]);
}
return intersecting;
}
bool intersectFrustum(const glm::mat4x4& view_projection, const AABB& aabb)
{
std::vector<AABB> aabbs(1, aabb);
return intersectFrustum(view_projection, aabbs)[0];
}
// Indices for drawing the lines of the box / frustum
static const uint8_t indices[] = {0, 1, 1, 2, 2, 3, 3, 0,
4, 5, 5, 6, 6, 7, 7, 4,
0, 4, 1, 5, 2, 6, 3, 7};
void drawFrustum(const glm::mat4x4& view_projection, const glm::vec3& color)
{
// http://donw.io/post/frustum-point-extraction
glm::mat4x4 clip_to_world = glm::inverse(view_projection);
glm::vec4 frustum[8] =
{
{-1, -1, -1, 1}, // 0
{ 1, -1, -1, 1}, // 1
{ 1, 1, -1, 1}, // 2
{-1, 1, -1, 1}, // 3
{-1, -1, 1, 1}, // 4
{ 1, -1, 1, 1}, // 5
{ 1, 1, 1, 1}, // 6
{-1, 1, 1, 1} // 7
};
for (int i = 0; i < 8; i++)
{
frustum[i] = clip_to_world * frustum[i];
frustum[i] /= frustum[i].w;
}
glColor3fv(&color.r);
glEnableClientState(GL_VERTEX_ARRAY);
glVertexPointer(4, GL_FLOAT, 0, frustum);
glDrawElements(GL_LINES, 24, GL_UNSIGNED_BYTE, indices);
glDisableClientState(GL_VERTEX_ARRAY);
}
void drawAABB(const AABB& box, const glm::vec3& color)
{
const float v[] = {box.min.x, box.min.y, box.min.z, 1, // 0
box.max.x, box.min.y, box.min.z, 1, // 1
box.max.x, box.max.y, box.min.z, 1, // 2
box.min.x, box.max.y, box.min.z, 1, // 3
box.min.x, box.min.y, box.max.z, 1, // 4
box.max.x, box.min.y, box.max.z, 1, // 5
box.max.x, box.max.y, box.max.z, 1, // 6
box.min.x, box.max.y, box.max.z, 1}; // 7
glColor3fv(&color.r);
glEnableClientState(GL_VERTEX_ARRAY);
glVertexPointer(4, GL_FLOAT, 0, v);
glDrawElements(GL_LINES, 24, GL_UNSIGNED_BYTE, indices);
glDisableClientState(GL_VERTEX_ARRAY);
}
AABB aabb;
glm::mat4x4 left_camera_pose;
glm::mat4x4 left_projection;
glm::mat4x4 right_camera_pose;
glm::mat4x4 right_projection;
float left_aspect = 1.2;
bool left_is_current = true;
Viewport viewport;
glm::vec2 cursor_position = glm::vec2(0, 0);
glm::vec2 previous_cursor_position = glm::vec2(0, 0);
void render(GLFWwindow* window)
{
const glm::mat4x4 left_view = glm::inverse(left_camera_pose);
const glm::mat4x4 left_view_projection = left_projection * left_view;
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
// Draw line separating the viewports
{
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glViewport(viewport.x, viewport.y, viewport.width, viewport.height);
const float x = (left_aspect / (left_aspect + 1)) * 2 - 1;
glColor3f(1, 1, 1);
glBegin(GL_LINES);
glVertex2f(x, -1);
glVertex2f(x, 1);
glEnd();
}
const glm::vec3 aabb_color = intersectFrustum(left_view_projection, aabb) ? glm::vec3(0, 1, 0) : glm::vec3(1, 0, 0);
// Draw into left viewport
{
Viewport left_viewport;
left_viewport.x = viewport.x;
left_viewport.y = viewport.y;
left_viewport.width = (left_aspect / (left_aspect + 1)) * viewport.width;
left_viewport.height = viewport.height;
glViewport(left_viewport.x, left_viewport.y, left_viewport.width, left_viewport.height);
glMatrixMode(GL_MODELVIEW);
glLoadMatrixf(&left_view[0][0]);
glMatrixMode(GL_PROJECTION);
glLoadMatrixf(&left_projection[0][0]);
// Draw aabb
drawAABB(aabb, aabb_color);
// Draw origin
glBegin(GL_LINES);
glColor3f(1, 0, 0); glVertex3f(0, 0, 0); glVertex3f(1, 0, 0);
glColor3f(0, 1, 0); glVertex3f(0, 0, 0); glVertex3f(0, 1, 0);
glColor3f(0, 0, 1); glVertex3f(0, 0, 0); glVertex3f(0, 0, 1);
glEnd();
}
// Draw into right viewport
{
Viewport right_viewport;
right_viewport.x = (left_aspect / (left_aspect + 1)) * viewport.width;
right_viewport.y = viewport.y;
right_viewport.width = (1 - left_aspect / (left_aspect + 1)) * viewport.width;
right_viewport.height = viewport.height;
glViewport(right_viewport.x, right_viewport.y, right_viewport.width, right_viewport.height);
const glm::mat4x4 model_view = glm::inverse(right_camera_pose);
glMatrixMode(GL_MODELVIEW);
glLoadMatrixf(&model_view[0][0]);
glMatrixMode(GL_PROJECTION);
glLoadMatrixf(&right_projection[0][0]);
// Draw aabb
drawAABB(aabb, aabb_color);
// Draw origin
glBegin(GL_LINES);
glColor3f(1, 0, 0); glVertex3f(0, 0, 0); glVertex3f(1, 0, 0);
glColor3f(0, 1, 0); glVertex3f(0, 0, 0); glVertex3f(0, 1, 0);
glColor3f(0, 0, 1); glVertex3f(0, 0, 0); glVertex3f(0, 0, 1);
glEnd();
// Draw left camera coordiante system
const glm::vec4 o = left_camera_pose * glm::vec4(0, 0, 0, 1);
const glm::vec4 x = o + left_camera_pose * glm::vec4(1, 0, 0, 0);
const glm::vec4 y = o + left_camera_pose * glm::vec4(0, 1, 0, 0);
const glm::vec4 z = o + left_camera_pose * glm::vec4(0, 0, 1, 0);
glBegin(GL_LINES);
glColor3f(1, 0, 0); glVertex3fv(&o.x); glVertex3fv(&x.x);
glColor3f(0, 1, 0); glVertex3fv(&o.x); glVertex3fv(&y.x);
glColor3f(0, 0, 1); glVertex3fv(&o.x); glVertex3fv(&z.x);
glEnd();
// Draw frustum from left_camera
drawFrustum(left_view_projection, glm::vec3(1, 1, 1));
}
glfwSwapBuffers(window);
}
void framebufferSizeCallback(GLFWwindow* window, int width, int height)
{
viewport.x = 0;
viewport.y = 0;
viewport.width = width;
viewport.height = height;
glViewport(0, 0, width, height);
render(window);
}
glm::vec2 windowToFramebufferCoordinates(GLFWwindow* window, double x, double y)
{
int window_width, window_height;
glfwGetWindowSize(window, &window_width, &window_height);
int fb_width, fb_height;
glfwGetFramebufferSize(window, &fb_width, &fb_height);
return glm::vec2(fb_width * x / window_width, fb_height * (1 - y / window_height));
}
void mouseButtonCallback(GLFWwindow* window, int button, int action, int mods)
{
double x, y;
glfwGetCursorPos(window, &x, &y);
previous_cursor_position = windowToFramebufferCoordinates(window, x, y);
left_is_current = previous_cursor_position.x < (left_aspect / (left_aspect + 1)) * viewport.width;
}
void cursorPosCallback(GLFWwindow* window, double x, double y)
{
cursor_position = windowToFramebufferCoordinates(window, x, y);
const glm::vec2 cursor_direction = cursor_position - previous_cursor_position;
previous_cursor_position = cursor_position;
if (viewport.width == 0 || viewport.height == 0)
{
return;
}
const bool left_pressed = glfwGetMouseButton(window, GLFW_MOUSE_BUTTON_LEFT) == GLFW_PRESS;
if (left_pressed)
{
glm::mat4x4& camera_pose = left_is_current ? left_camera_pose : right_camera_pose;
const float cursor_distance = glm::length(cursor_direction);
const float minimum_cursor_distance = 0.1;
if (cursor_distance < minimum_cursor_distance)
{
return;
}
glm::mat3x3 rotation;
for (int x = 0; x < 3; ++x)
{
for (int y = 0; y < 3; ++y)
{
rotation[x][y] = camera_pose[x][y];
}
}
const glm::vec3 ex = glm::vec3(1, 0, 0);
const glm::vec3 ey = glm::vec3(0, 1, 0);
const float viewport_diagonal = glm::length(glm::vec2(viewport.width, viewport.height));
const float rotation_angle = 7 * std::atan(cursor_distance / viewport_diagonal);
const glm::vec3 rotation_axis = glm::normalize(cursor_direction.x * (rotation * ey) - cursor_direction.y * (rotation * ex));
const glm::mat4x4 dR = glm::toMat4(glm::angleAxis(rotation_angle, rotation_axis));
const glm::vec3 pivot = camera_pose[3];
const glm::mat4x4 t1 = glm::translate(glm::mat4x4(1), -pivot);
const glm::mat4x4 t2 = glm::translate(glm::mat4x4(1), pivot);
camera_pose = glm::inverse(t2 * dR * t1) * camera_pose;
render(window);
}
}
void keyCallback(GLFWwindow* window, int key, int scancode, int action, int mods)
{
if (action == GLFW_PRESS || action == GLFW_REPEAT)
{
const bool shift_pressed = (mods & GLFW_MOD_SHIFT);
bool should_render = true;
if (key == GLFW_KEY_A || key == GLFW_KEY_D || key == GLFW_KEY_W || key == GLFW_KEY_S || key == GLFW_KEY_Q || key == GLFW_KEY_E)
{
const float distance = shift_pressed ? 5 : 1;
glm::vec3 translation = glm::vec3(0, 0, 0);
switch (key)
{
case GLFW_KEY_A: translation.x -= distance; break;
case GLFW_KEY_D: translation.x += distance; break;
case GLFW_KEY_W: translation.z -= distance; break;
case GLFW_KEY_S: translation.z += distance; break;
case GLFW_KEY_Q: translation.y -= distance; break;
case GLFW_KEY_E: translation.y += distance; break;
}
glm::mat4x4& camera_pose = left_is_current ? left_camera_pose : right_camera_pose;
camera_pose = glm::translate(camera_pose, translation);
}
else if (key == GLFW_KEY_SPACE)
{
right_camera_pose = left_camera_pose;
}
else
{
should_render = false;
}
if (should_render)
{
render(window);
}
}
}
int main(int argc, char** argv)
{
if (!glfwInit())
{
std::cerr << "Could not initialize GLFW\n";
return EXIT_FAILURE;
}
GLFWwindow* window;
{
const int height = 600;
const int width = height * left_aspect + height;
window = glfwCreateWindow(width, height, "Frustum Culling", nullptr, nullptr);
if (!window)
{
std::cerr << "Could not create a glfw window " << width << " " << height << "\n";
glfwTerminate();
return EXIT_FAILURE;
}
}
glfwSetFramebufferSizeCallback(window, framebufferSizeCallback);
glfwSetMouseButtonCallback(window, mouseButtonCallback);
glfwSetCursorPosCallback(window, cursorPosCallback);
glfwSetKeyCallback(window, keyCallback);
// Initialize rendering
glfwMakeContextCurrent(window);
glEnable(GL_DEPTH_TEST);
glClearColor(0.1, 0.1, 0.1, 1);
aabb.min = glm::vec3(-3, -5, -4);
aabb.max = glm::vec3(6.5, 6, 4.5);
left_camera_pose = glm::inverse(glm::lookAt(glm::vec3(1, 0.5, 20), 0.5f * (aabb.min + aabb.max), glm::vec3(0, 1, 0)));
right_camera_pose = glm::inverse(glm::lookAt(glm::vec3(10, 5, 30), 0.5f * (aabb.min + aabb.max), glm::vec3(0, 1, 0)));
left_projection = glm::perspective(static_cast<float>(45 * M_PI / 180), left_aspect, 5.0f, 30.0f);
right_projection = glm::perspective(static_cast<float>(60 * M_PI / 180), 1.0f, 0.05f, 100.0f);
// Render
{
int width, height;
glfwGetFramebufferSize(window, &width, &height);
framebufferSizeCallback(window, width, height);
}
while (!glfwWindowShouldClose(window))
{
glfwWaitEvents();
}
glfwTerminate();
return EXIT_SUCCESS;
}
CMakeLists.txt
cmake_minimum_required(VERSION 3.15)
project(frustum_culling)
set(CMAKE_CXX_STANDARD 14)
set(CMAKE_CXX_STANDARD_REQUIRED ON)
find_package(glm CONFIG REQUIRED)
find_package(glfw3 3.3 CONFIG REQUIRED)
find_package(OpenGL REQUIRED)
add_library(opengl INTERFACE)
target_link_libraries(opengl INTERFACE ${OPENGL_gl_LIBRARY})
target_compile_definitions(opengl INTERFACE -DGL_SILENCE_DEPRECATION)
add_executable(frustum_culling frustum_culling.cpp)
target_link_libraries(frustum_culling glfw glm::glm opengl)