Hi,
I have caculatated the geometric product of two lines with the hope that I can extract easily the angle between the lines and the point-pair with describes the shortest distance between the two(skewed) lines. I have found the cos of the angle between the lines as the scalar component but it look more difficult to get the sin to be able to to compute the atan2() to get the angle in the full range with the complete sign. To get the point pair I have no idea for easy computation. I think the resulting three-vector should describe somehow the direction of the line where the two points are laying on.
Any idea or hint to paper to follow?
best regards
Oliver
Hereʻs a sketch of how I solved this problem. I am using a kind of programming syntax to describe the method. I rely heavily on projecting a point onto a line using (P . L) / L. Projecting P onto L gives the point on L closest to P.
-
Start with lines L1 and L2, and make N1 the normal along L1. Hint: V1 = -e45 . L; N1 = V1 / Mag(V1).
-
Select P0 as an arbitrary point on L1. Hint: you can project eo onto L1; if you get 0 then eo is on L1, so you can set P0 = eo.
-
Make a translator T(s) = 1 - 0.5 * s * N1 * ei
-
define P1(s) = T(s) * P0 * Rev(T(s))
// point P1(s) is on line L1 -
define P2(s) = (P1(s) << L2) / L2
// point P2(s) is projection of P1(s) on line L2 -
define D(s) = -2 * (P1(s) . P2(s))
// D(s) is the distance squared from P1(s) to P2(s)
// D(s) should be a quadratic in s; d = axx + b*x + c -
Solve for s at the minimum of D(s), which is the axis of the parabola at s = -0.5*b/a.
-
Evaluate P1(s) and P2(s) using the calculated s. These are your solution points.
The resulting points should be normalized, providing that the points used to construct L1 and L2 were normalized. This makes it easy to extract the 3D vectors, but you might have a value for the ei component that is not 0.5vv. This is a bit puzzling to me, but it does not seem to affect the validity of the points.
In a case like this, I’m curious whether it might not make sense to shift over to 3D euclidean PGA to solve this problem, since it is one dimension lower than euclidean CGA.
For the purposes of comparison I work out the solution in this post.
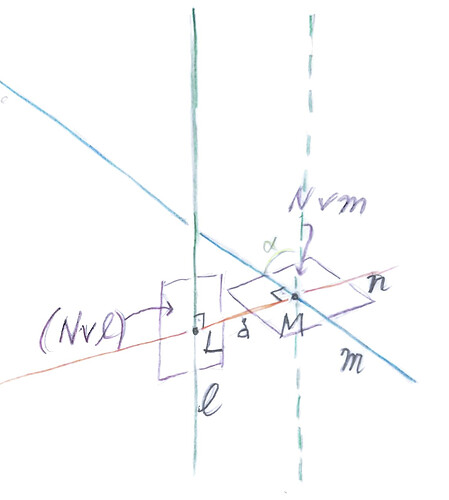
Let the two normalized euclidean lines be \bf{l} and \bf{m}. In the generic case (that is, the two lines are not parallel), they have unique common normal line \bf{n}. Then the tasks posed in the post are to find
- the common normal line \mathbf{n},
- the angle \alpha between \bf{l} and \bf{m} when viewed along \bf{n}, in the range [0, 2\pi),
- the distance d between the lines measured along \bf{n}, and
- the intersection points \bf{L} and \bf{M} where \bf{n} cuts \bf{l}, resp., \bf{m}.
Consult the following drawing:
The geometric product breaks into three pieces: \\ \bf{lm} = g_0 + g_2 + g_4 where \bf{g}_i = \langle \bf{lm} \rangle_i.
In particular,
\\ g_0 = \cos{\alpha},
\\g_2 = \sin{\alpha} ~\mathbf{n} + d\cos{\alpha}~\bf{n}^\perp, and
\\g_4 = d \sin{\alpha} ~\mathbf{I}
Here \mathbf{n}^\perp = \mathbf{nI} is the polar line of \mathbf{n}.
(For details see the course notes for the SIGGRAPH 2019 course “Geometric Algebra for Computer Graphics”, Sec. 8.1, available here).
For convenience define p to be the coefficient of \mathbf{I} in g_4 (i. e., p := d \sin{\alpha}).
The tasks can then be solved in 3D euclidean PGA as follows:
- \mathbf{n} is the axis of the bivector g_2, extract it using Sec. 8.1.3 of the course notes.
- \alpha = (p >= 0) ~~?~~ \cos^{-1}({g_0}) : (2 \pi -\cos^{-1}({g_0})) . Then \alpha \in [0, 2\pi).
- d = (\alpha \neq 0) ~~?~~ \dfrac{p}{\sin{\alpha}} : | \mathbf{n}^\perp |_\infty.
- Let \mathbf{N} := \mathbf{n} \wedge \mathbf{e}_0 be the ideal point of \mathbf{n}. Then \\\mathbf{L} := (\mathbf{N} \vee \mathbf{m})\wedge \mathbf{l}, and \\\mathbf{M} := (\mathbf{N} \vee \mathbf{l})\wedge \mathbf{m}.
Exercise Show that \mathbf{n}^\perp = \mathbf{L}_\infty \vee \mathbf{M}_\infty where \mathbf{L}_\infty and \mathbf{M}_\infty are the ideal points of \mathbf{l}, resp., \mathbf{m}.
Example WLOG we can assume that the coordinate system has been chosen so that:
\\ \mathbf{l} = \mathbf{e}_{12}, the vertical line through the origin, and
\\\mathbf{m} = (d \mathbf{e}_0 - \mathbf{e}_1) \wedge (\sin{\alpha}~\mathbf{e}_3 + \cos{\alpha}~\mathbf{e}_2) = d(\cos{\alpha}~ \mathbf{e}_{02} + \sin{\alpha}~ \mathbf{e}_{03}) - \cos{\alpha}~ \mathbf{e}_{12} + \sin{\alpha} ~\mathbf{e}_{31}
a line in the plane x=d that makes an angle of \alpha with the positive z-direction.
Consult the figure to verify that that in this case \\\mathbf{n} = \mathbf{e}_{23}, \mathbf{n}^\perp = \mathbf{e}_{01}, \mathbf{N} = \mathbf{e}_{032}, \mathbf{L} = \mathbf{e}_{123} and \mathbf{M} = \mathbf{e}_{123} + d \mathbf{e}_{032}.
We now verify that the formulas verify these observations.
Letting c:= \cos{\alpha} and s := \sin{\alpha} and calculating yields:
\\\mathbf{lm} = (\mathbf{e}_{12})((d \mathbf{e}_0 - \mathbf{e}_1) \wedge (s\mathbf{e}_3 + c\mathbf{e}_2))
~~~~~~= (\mathbf{e}_{12})(s\mathbf{e}_{31} - c\mathbf{e}_{12} + d s \mathbf{e}_{03} + d c \mathbf{e}_{02})
~~~~~~= s\mathbf{e}_{23} + c + + d s \mathbf{I} + d c \mathbf{e}_{01}
~~~~~~=c+(s\mathbf{e}_{23} + d c \mathbf{e}_{01}) + d s \mathbf{I}
This agrees with the observations made above.
To verify the formulas for \mathbf{L} and \mathbf{M} we calculate:
\\\mathbf{L} = (\mathbf{N}\vee \mathbf{m})\wedge \mathbf{l} = s(c \mathbf{e}_2 + s \mathbf{e}_3) \wedge \mathbf{e}_{12} = s^2 \mathbf{e}_{123} \cong \mathbf{e}_{123}
\\\mathbf{M} = (\mathbf{N}\vee \mathbf{l})\wedge \mathbf{m} = -s \mathbf{e}_2 \wedge (s\mathbf{e}_{31} - c\mathbf{e}_{12} + d s \mathbf{e}_{03} + d c \mathbf{e}_{02}) = -s^2(d \mathbf{e}_{032}+\mathbf{e}_{123}) \cong d \mathbf{e}_{032}+\mathbf{e}_{123}
Hi Charles,
very thanks for your solution in PGA. In the meantime I found a solution in CGA and it looks interesting to me to compare both solutions. I have also started to solve some further simple geometric problems with CGA and to compare it with PGA. The first answer I got on my original question here, seems also to work but looks a bit complicated. Some years ago I solve the problem based on plücker coordinates and there I run into the problem that I need to switch between different cases. One case was that one line gos through the origin. I think I have not completely understood how this correspond to the PGA solution. Maybe I will find some time to have a closer look at this next week.Than I can also write the CGA solution here to compare it.
best regards
Oliver